
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
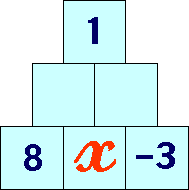
Dans la pyramide ci-dessus, le nombre dans une case est la
somme
des nombres placés en dessous d'elle. Quelle est donc la valeur de x ? |
|
|
On suppose maintenant que
le nombre dans une case est la
différence
-de
gauche à
droite- des nombres
placés en dessous d'elle. Quelle est alors la valeur de x ? |
|
|
Que remarquez-vous quant
aux résultats trouvés en 1° et 2° ?
Et si c'était le cas quels que soient les nombres
donnés ? ➔ Remplacez 1 par a, 8 par b et -3 par c... |
Si vous séchez près avoir bien cherché : ››››
| Solution : |
|
Nous avons (8 + x) + (x - 3) = 1, ce
qui fournit : x =
2 |
|
|
(8 - x) - [x -(- 3)] = 1, ce qui fournit : x = -2
!
si
les () n'ont pas un rôle fondamental en addition, elles en ont un
en soustraction... |
|
|
On constate ci-dessus
que les solutions sont opposées. Est-ce généralement le cas ?
x = (-a + b + c)/2 ➔ On constate que les solutions sont opposées : le cas est général. |