ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
La loi de Pareto exprime que le nombre N de contribuables soumis à un impôt r sur le revenu, dans une société donnée et pour une période donnée, est une fonction puissance décroissante du revenu, c'est dire qu'il existe deux nombres positifs a et k tel que :

Vérifions cette loi de régression "puissance" sur un exemple :
Une étude statistique portant sur le revenu annuel des contribuables soumis à l'impôt sur les salaires en 1984 dans un pays X... d'Afrique francophone faisait ressortir le tableau suivant :
|
|
|
|
(en milliers) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En utilisant le logarithme décimal (log) et 2 cm comme unité en abscisse et ordonnée, on représente le nuage de points Mi(Xi,Yi) définis par Xi = log ri , Yi = log Ni. On constate, ci-contre, un très bon alignement de ces points.

En ajustant ce nuage par la droite de Y en X par
la méthode des moindres carrés, au moyen d'une
calculatrice de poche (c'est autorisé!), on obtient rapidement (arrondis
à 10-4)
:
Un résultat que nous arrondissons au centième, soit :
c'est à dire en fait : log N = -1,53log(r) +5,69 = log(r-1,53) + 5,69
On en déduit :
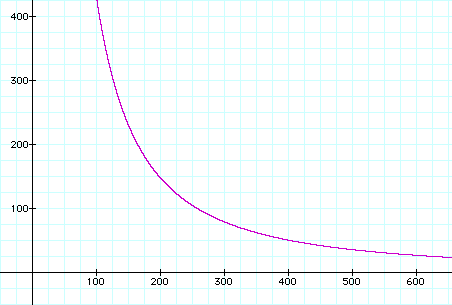
et, ci-dessous, la représentation de N en fonction de r : la courbe s'ajuste parfaitement aux données.