
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Combien comptez-vous de parallélogrammes dans cette figure ?
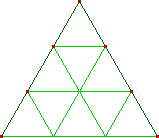 Trop facile, d'accord ?
Trop facile, d'accord ?Alors on essaye avec :
 C'était
plus long mais faisable, non ?..
C'était
plus long mais faisable, non ?..
Et enfin, avec :

Si tu sèches après avoir bien cherché : ››››
| Solution : |
Il y a 3 types de parallélogrammes. Ceux qui ont :
Mais par rotations successives (dans le sens des aiguilles d'une montre, par exemple), on voit que les cas 2 et 3 deviennent le cas 1. Dénombrons donc les parallélogrammes du cas 1 et multiplions par 3.
|
1er cas/ (3 sur 3) : |
Base simple :
|
dimensions |
col=1 |
col= 2 |
col= 3 |
|
haut=1 |
2 |
1 |
0 |
|
haut= 2 |
1 |
0 |
0 |
Base double :
|
dimensions |
col=1+2 |
col= 2+3 |
|
haut=1 |
1 |
0 |
|
haut= 2 |
0 |
0 |
Base triple : néant.
Donc en tout : (4 + 1) × 3 = 15 parallélogrammes
| 2ème cas/ (4 sur 4) : |
Base simple :
|
dimensions |
col=1 |
col= 2 |
col= 3 |
col= 4 |
|
haut=1 |
3 |
2 |
1 |
0 |
|
haut= 2 |
2 |
1 |
0 |
|
|
haut= 3 |
1 |
0 |
||
|
haut= 4 |
0 |
Total : 10 |
Base double :
|
dimensions |
col=1+2 |
col= 2+3 |
col= 3+4 |
|
haut=1 |
2 |
1 |
0 |
|
haut= 2 |
1 |
0 |
1 |
|
haut= 3 |
0 |
Total : 5 |
Base triple :
|
dimensions |
col=1+2+3 |
col= 2+3+4 |
|
haut=1 |
1 |
0 |
|
haut= 2 |
0 |
Total : 1 |
Base quadruple : néant
Donc en tout : (10 + 5 + 1) × 3 = 48 parallélogrammes
| 3ème cas/ (6 sur 6) : |
Base simple :
|
dimensions |
col=1 |
col= 2 |
col= 3 |
col= 4 |
col= 5 |
col= 6 |
|
haut=1 |
5 |
4 |
3 |
2 |
1 |
0 |
|
haut= 2 |
4 |
3 |
2 |
1 |
0 |
|
|
haut= 3 |
3 |
2 |
1 |
0 |
||
|
haut= 4 |
2 |
1 |
0 |
|||
|
haut= 5 |
1 |
0 |
||||
|
sous-totaux |
15 |
10 |
6 |
3 |
1 |
Total = 35 |
Base double :
|
dimensions |
col=1+2 |
col= 2+3 |
col= 3+4 |
col= 4+5 |
col= 5+6 |
|
haut=1 |
4 |
3 |
2 |
1 |
0 |
|
haut= 2 |
3 |
2 |
1 |
0 |
|
|
haut= 3 |
2 |
1 |
0 |
||
|
haut= 4 |
1 |
0 |
|||
|
haut= 5 |
0 |
||||
|
sous-totaux |
10 |
6 |
3 |
1 |
Total = 20 |
Base triple :
|
dimensions |
col=1+2+3 |
col= 2+3+4 |
col= 3+4+5 |
col= 4+5+6 |
|
haut=1 |
3 |
2 |
1 |
0 |
|
haut= 2 |
2 |
1 |
0 |
|
|
haut= 3 |
1 |
0 |
||
|
haut= 4 |
0 |
|||
|
sous-totaux |
6 |
3 |
1 |
Total = 10 |
Base quadruple :
|
dimensions |
col=1+2+3+4 |
col= 2+3+4+5 |
col= 3+4+5+6 |
|
haut=1 |
2 |
1 |
0 |
|
haut= 2 |
1 |
0 |
|
|
haut= 3 |
0 |
||
|
sous-totaux |
3 |
1 |
Total = 4 |
Base quintuple :
|
dimensions |
col=1+2+3+4+5 |
col= 2+3+4+5+6 |
|
haut=1 |
1 |
0 |
|
haut= 2 |
0 |
|
|
sous-totaux |
1 |
Total = 1 |
Nous dénombrons ainsi : 35 + 20 + 10 + 4 + 1 = 70 parallélogrammes
En conclusion, il y a donc 210 parallélogrammes dans cette figure. Ouf !