
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Voici ci-dessous un cône pouvant, par exemple, contenir de la crème glacée; il prend alors le nom de cornet (petite corne).

Si vous voulez partager équitablement ce cornet avec l'un de vos proches, à quelle distance de son sommet devriez-vous le couper (section perpendiculaire à l'axe du cône) ?
Attention : la figure est peut-être trompeuse...
| Solution : |
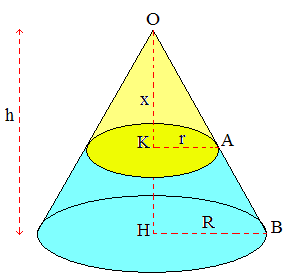
Notons x = OK la distance de la section par rapport au sommet O, h la hauteur du cône, r le rayon de la section et R celui de la base.
Le volume du cône (cornet entier) est :
![]()
Le volume du cône obtenu par section (en jaune) est :
![]()
Nous voulons l'égalité :

C'est à dire :
2r2x = R2h ou encore : 2r2 x x/h = R2 (r1)
Or, selon la propriété de Thalès appliquée dans le triangle OHB, coupé par [AK] parallèle au côté [HB], on peut écrire :
OK/OH = AK/HB , soit : x/h = r/R
En remplaçant x/h par r/R, dans la relation (r1), on obtient :
2x3 = h3
Un peu de cours :
♦ Deux nombres égaux a = b, ont des cubes égaux : a3 = b3. Inversement, selon la règle des signes, si deux cubes sont égaux : a3 = b3, alors les nombres sont égaux : a = b. Ce qui n'est pas nécessairement le cas pour les carrés : si a2 = b2, on peut aussi avoir a = - b.
(1,26)3 = 2,000376 : on voit que le cube de 1,26 est très voisin de 2.
♦ Par approximations successives, on peut trouver une approximation du nombre r tel que r3 = 2 : ce nombre r est appelé racine cubique de 2.
♦ Plus généralement, tout nombre r tel que r3 = a est la racine cubique du nombre a (a quelconque positif ou non).
Par exemple, 3 est la racine cubique de 27;
-2 est la racine cubique de -8;
1/2 est la racine cubique de 1/8
le produit ab est la racine cubique du produit a3b3.

Revenons à notre exercice : soit r la racine cubique de 2, on a : r3x3 = h3, donc rx = h, et par suite : x = h/r, ou encore :
|
|
On voit qu'il faut couper "très bas"... : presque au 4/5 de la hauteur !

Question subsidiaire :
si vous aviez partagé le cornet en deux à la moitié
de sa hauteur, à quelle fraction aurait correspondu la partie conique (en jaune)
?
Rép. : 1/8. On
est loin de la moitié ! en effet, il s'agit ici d'une réduction d'échelle 1/2 :
les volumes subissent une réduction de coefficient (1/2)3 = 1/8.
